Dimensionality reduction and PCA

PCA is unsupervised learning (contains no label information). It is usually used to explore data and understand patterns and used to set up clustering analysis.

Objective of clustering is to find patterns and relationships within a dataset, such as: - Geometric (feature distances) - Connectivity (spectral clustering, graphs)

However, the original dimensionally {R^n} can be large! The goal is to reduce it, k≪n!

Dimensionality reduction is the process of reducing the number of random variables under consideration - Combine, transform or select variables - Can use linear or nonlinear operations

PCA, or prinicpal component analysis, is one common way to perform dimensionality reduction. Dimensionality reduction has many uses in data science: - Visualizing, exploring and understanding the data - Extracting ”features” and dominant modes - Cleaning data - Speeding up subsequent learning task - Building simpler model later

It has many practical applications as well, such as image/audio compression, face recognition, and natural language processing (latent semantic analysis) to name a few!

PCA, by hand

Step 1: Normalize

Normalize (sometimes called scaling and/or standardizing) your data, especially if the different dimensions contain different scales of data.

Step 2: Estimate the mean and covariance matrix from the data

The covariance matrix, C, captures the variability of the data points along different directions, it also captures correlations, covariance between different coordinates (features in the x vector).

Step 3: Take the largest K eigenvectors of C which correspond to the largest eigenvalues

Use a solver for this part, such as {eigs} function from scipy.sparse.linalg. In this case, I used K=2 to reduce the data to 2 dimensions.

C=UΛU^T

C has d×d dimensions

U=eigenvectors

Step 4: Compute the reduced representation of a data point

Key Concept: PCA is a form of linear reduction scheme, because the prinicpal component \(z_i\) is linear transformation of the x.

Food consumption in European countries

This anaylsis uses PCA to compare European countries consumption of various food and drink.

Libraries

import numpy as np
import pandas as pd
import math
import matplotlib.pyplot as plt
import scipy.io as spio
import scipy.sparse.linalg as ll
import sklearn.preprocessing as skpp

Load and Prep Data

# Import CSV and save it in different dataframes
food_consumption = pd.read_csv("data/food-consumption.csv")
display(food_consumption)

# pull out country list
countries = food_consumption['Country']
#display(countries)

# remove country column, convert to array
Anew = food_consumption.drop(columns=['Country']).to_numpy()
#display(Anew)

# get shape of matrix
m, n = Anew.shape

	Country	Real coffee	Instant coffee	Tea	Sweetener	Biscuits	Powder soup	Tin soup	Potatoes	Frozen fish	...	Apples	Oranges	Tinned fruit	Jam	Garlic	Butter	Margarine	Olive oil	Yoghurt	Crisp bread
0	Germany	90	49	88	19	57	51	19	21	27	...	81	75	44	71	22	91	85	74	30	26
1	Italy	82	10	60	2	55	41	3	2	4	...	67	71	9	46	80	66	24	94	5	18
2	France	88	42	63	4	76	53	11	23	11	...	87	84	40	45	88	94	47	36	57	3
3	Holland	96	62	98	32	62	67	43	7	14	...	83	89	61	81	15	31	97	13	53	15
4	Belgium	94	38	48	11	74	37	23	9	13	...	76	76	42	57	29	84	80	83	20	5
5	Luxembourg	97	61	86	28	79	73	12	7	26	...	85	94	83	20	91	94	94	84	31	24
6	England	27	86	99	22	91	55	76	17	20	...	76	68	89	91	11	95	94	57	11	28
7	Portugal	72	26	77	2	22	34	1	5	20	...	22	51	8	16	89	65	78	92	6	9
8	Austria	55	31	61	15	29	33	1	5	15	...	49	42	14	41	51	51	72	28	13	11
9	Switzerland	73	72	85	25	31	69	10	17	19	...	79	70	46	61	64	82	48	61	48	30
10	Sweden	97	13	93	31	61	43	43	39	54	...	56	78	53	75	9	68	32	48	2	93
11	Denmark	96	17	92	35	66	32	17	11	51	...	81	72	50	64	11	92	91	30	11	34
12	Norway	92	17	83	13	62	51	4	17	30	...	61	72	34	51	11	63	94	28	2	62
13	Finland	98	12	84	20	64	27	10	8	18	...	50	57	22	37	15	96	94	17	21	64
14	Spain	70	40	40	18	62	43	2	14	23	...	59	77	30	38	86	44	51	91	16	13
15	Ireland	30	52	99	11	80	75	18	2	5	...	57	52	46	89	5	97	25	31	3	9

16 rows × 21 columns

Normalize data

In this case, we normalize the data because features have very different ranges

stdA = np.std(Anew,axis = 0)
Anew = Anew @ np.diag(np.ones(stdA.shape[0])/stdA)
Anew = Anew.T

#display(pd.DataFrame(Anew))

PCA

Here, we extract the first two dimensions following the steps listed above.

mu = np.mean(Anew,axis = 1)
xc = Anew - mu[:,None]

C = np.dot(xc,xc.T)/m

K=2
S,W = ll.eigs(C,k = K)
S = S.real
W = W.real

dim1 = np.dot(W[:,0].T,xc)/math.sqrt(S[0]) # extract 1st eigenvalues
dim2 = np.dot(W[:,1].T,xc)/math.sqrt(S[1]) # extract 2nd eigenvalue

Plot 1

The location of the countries does seem logical (countries close to one another are likely to consume similar foods) – Nordic countries are grouped together, as are countries in the S-SW (Portugal, Spain, Italy) with a likely strong Mediterranean influence. Additionally, countries in central Europe are grouped (Germany, Belgium, Switzerland).

plt.figure(figsize=(7, 7))
plt.xlabel("dim1")
plt.ylabel("dim2")
plt.plot(dim1, dim2, 'r.')
plt.axvline(0, linewidth=0.5)
plt.axhline(0, linewidth=0.5)

# add labels
for i in range(0, countries.shape[0]):
    plt.text(dim1[i], dim2[i] + 0.01, countries[i])
plt.show()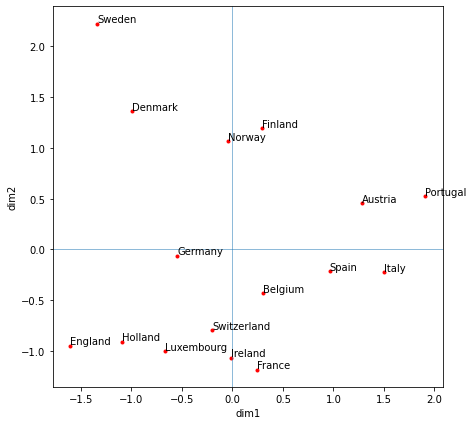

Check correlations to dim1 and dim2

Dimension 1 (PC 1) is highly correlated to countries with high consumption of tea, sweetener, tin soup, frozen veggies, and tinned fruit. Dimension 2 is highly correlated with high consumption of instant coffee, powder soup, and low consumption of frozen fish and crisp bread).

# add dim1 and dim2
food_consumption['dim1'] = dim1.tolist()
food_consumption['dim2'] = dim2.tolist()
display(food_consumption.drop(columns=['Country']).corr(method='pearson').tail(2).style.format('{0:,.2f}'))

	Real coffee	Instant coffee	Tea	Sweetener	Biscuits	Powder soup	Tin soup	Potatoes	Frozen fish	Frozen veggies	Apples	Oranges	Tinned fruit	Jam	Garlic	Butter	Margarine	Olive oil	Yoghurt	Crisp bread	dim1	dim2
dim1	0.08	0.43	0.70	0.78	0.58	0.43	0.77	0.51	0.51	0.75	0.61	0.51	0.88	0.68	-0.61	0.29	0.30	-0.38	0.21	0.43	1.00	0.00
dim2	-0.39	0.78	-0.09	-0.23	0.30	0.68	0.13	-0.36	-0.72	-0.54	0.48	0.26	0.35	0.13	0.36	0.13	-0.08	0.21	0.55	-0.76	0.00	1.00

Flipping the Analysis

In the analysis above, we looked at which countries were similar to one another based on their food consumptions. In the next set of analysis, we will look at how foods are related to another based on the countries were they are eaten.

If part 1 was comparing culinary culures by country, this next analysis can be thought of as comparing how common (or uncommon) food pairings are.

First, let’s treat this as a completely new problem and reset our notebook.

%reset -f

Libraries

import numpy as np
import pandas as pd
import math
import matplotlib.pyplot as plt
import scipy.io as spio
import scipy.sparse.linalg as ll
import sklearn.preprocessing as skpp

Load and Prep Data

# Import CSV and save it in different dataframes
food_consumption = pd.read_csv("data/food-consumption.csv")

# transpose df
food_consumption = food_consumption.set_index('Country').T.rename_axis(index='Food Item', columns=None).reset_index()
display(food_consumption)

# pull out country list
food_items = food_consumption['Food Item']
#display(food_items)

# remove food item column, convert to array
Anew = food_consumption.drop(columns=['Food Item']).to_numpy()
#display(Anew)

# get shape of matrix
m, n = Anew.shape

	Food Item	Germany	Italy	France	Holland	Belgium	Luxembourg	England	Portugal	Austria	Switzerland	Sweden	Denmark	Norway	Finland	Spain	Ireland
0	Real coffee	90	82	88	96	94	97	27	72	55	73	97	96	92	98	70	30
1	Instant coffee	49	10	42	62	38	61	86	26	31	72	13	17	17	12	40	52
2	Tea	88	60	63	98	48	86	99	77	61	85	93	92	83	84	40	99
3	Sweetener	19	2	4	32	11	28	22	2	15	25	31	35	13	20	18	11
4	Biscuits	57	55	76	62	74	79	91	22	29	31	61	66	62	64	62	80
5	Powder soup	51	41	53	67	37	73	55	34	33	69	43	32	51	27	43	75
6	Tin soup	19	3	11	43	23	12	76	1	1	10	43	17	4	10	2	18
7	Potatoes	21	2	23	7	9	7	17	5	5	17	39	11	17	8	14	2
8	Frozen fish	27	4	11	14	13	26	20	20	15	19	54	51	30	18	23	5
9	Frozen veggies	21	2	5	14	12	23	24	3	11	15	45	42	15	12	7	3
10	Apples	81	67	87	83	76	85	76	22	49	79	56	81	61	50	59	57
11	Oranges	75	71	84	89	76	94	68	51	42	70	78	72	72	57	77	52
12	Tinned fruit	44	9	40	61	42	83	89	8	14	46	53	50	34	22	30	46
13	Jam	71	46	45	81	57	20	91	16	41	61	75	64	51	37	38	89
14	Garlic	22	80	88	15	29	91	11	89	51	64	9	11	11	15	86	5
15	Butter	91	66	94	31	84	94	95	65	51	82	68	92	63	96	44	97
16	Margarine	85	24	47	97	80	94	94	78	72	48	32	91	94	94	51	25
17	Olive oil	74	94	36	13	83	84	57	92	28	61	48	30	28	17	91	31
18	Yoghurt	30	5	57	53	20	31	11	6	13	48	2	11	2	21	16	3
19	Crisp bread	26	18	3	15	5	24	28	9	11	30	93	34	62	64	13	9

Normalize data

# In this case, we normalize the data because features have very different ranges
stdA = np.std(Anew,axis = 0)
Anew = Anew @ np.diag(np.ones(stdA.shape[0])/stdA)
Anew = Anew.T

#display(pd.DataFrame(Anew))

PCA

mu = np.mean(Anew,axis = 1)
xc = Anew - mu[:,None]

C = np.dot(xc,xc.T)/m

K=2
S,W = ll.eigs(C,k = K)
S = S.real
W = W.real

dim1 = np.dot(W[:,0].T,xc)/math.sqrt(S[0]) # extract 1st eigenvalues
dim2 = np.dot(W[:,1].T,xc)/math.sqrt(S[1]) # extract 2nd eigenvalue

(20,)

Plot 2: Common (and uncommon) pairings

The location of the foods does seem logical (similar foods or ‘compatible’ foods are grouped together). Fresh fruit such as apples and oranges are grouped. So are common toppings such as jam, margarine, butter, and what they are put on (biscuits). Garlic and olive oil are loosely grouped and separated. Visually inspecting the graph, it seems that PC1 can be described as fish vs. high caffine (coffee, tea) intake and PC2 can be described by how much garlic and olive oil are apart of the diet for a country.

plt.figure(figsize=(7, 7))
plt.xlabel("dim1")
plt.ylabel("dim2")
plt.plot(dim1, dim2, 'r.')
plt.axvline(0, linewidth=0.5)
plt.axhline(0, linewidth=0.5)

# add labels
for i in range(0, food_items.shape[0]):
    plt.text(dim1[i], dim2[i] + 0.01, food_items[i])

plt.show()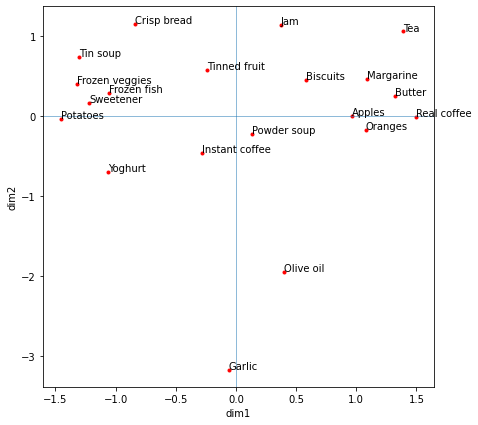

Check correlations to dim1 and dim2

Dimension 1 (PC 1) is highly correlated to food consumption areas like Germany, although it also has mild to strong correlations to many of the countries – indicating that this is indeed the dimension upon variation is maximized. Dimension 2 is most highly correlated to Sweden (positive) and Spain (negative).

# add dim1 and dim2
food_consumption['dim1'] = dim1.tolist()
food_consumption['dim2'] = dim2.tolist()
display(food_consumption.drop(columns=['Food Item']).corr(method='pearson').tail(2).style.format('{0:,.2f}'))

	Germany	Italy	France	Holland	Belgium	Luxembourg	England	Portugal	Austria	Switzerland	Sweden	Denmark	Norway	Finland	Spain	Ireland	dim1	dim2
dim1	0.95	0.80	0.80	0.70	0.90	0.86	0.60	0.73	0.89	0.82	0.49	0.82	0.84	0.80	0.73	0.70	1.00	0.00
dim2	0.13	-0.42	-0.32	0.33	-0.07	-0.33	0.40	-0.49	-0.13	-0.24	0.56	0.43	0.38	0.35	-0.60	0.31	0.00	1.00